Bridge Momentum: Understanding the Weight Component
Written by Chris Goodell | January 22, 2018
Take a look at the water surface profile in Figure 1 below. The two profiles are for Class A low flow (subcritical throughout) with identical boundary conditions, flow conditions, and geometry. The only difference is the bridge modeling approach: the blue line is calculated using the energy method; the red line is calculated using the momentum method. For this example, which is a simple rectangular channel, the difference in computed water surface elevation and energy grade line from the downstream cross-section to the upstream cross-section is 0.10 feet and 0.16 feet for the energy method, respectively; those differences increase to 1.64 feet and 1.64 feet, respectively, for the momentum method. Those of you well-versed in the applicability of the various bridge modeling approaches (see page 181 of the HEC-RAS River Analysis System, version 5.0,Hydraulic Reference Manual [Brunner, 2016] for a great discussion on this topic), will answer: “the momentum method accounts for the drag imparted by bridge piers on the flow and should be used when pier losses are significant; that’s why.” But check out Figure 2. There are no piers. The bridge doesn’t even touch the water surface!

Figure 1: Comparison of bridge modeling results between energy and momentum methods
Figure 2: Representative cross-section of modeled bridge
From a hydraulic perspective, the bridge is doing nothing in this model. We could ignore it, stick in two cross-sections, press “run”, use the tried-and-trusted energy equation, and be on our way. However, “momentum” has been as familiar and comfortable a term as “energy” ever since we first smashed two model cars in physics class. We know the one-dimensional form of the conservation of momentum equation backwards-and-forwards, have solved the above problem by hand in our open channel hydraulics class, and know that the momentum equation should give us an answer similar, if not identical, to the energy equation. Even though the title of this post gives away the reason for the difference, I’m going to let the suspense build and provide some background to understand the implementation of the momentum equation in HEC-RAS at bridges for steady discharge.
To calculate energy losses across the bridge using the momentum method, HEC-RAS performs three separate calculations of the conservation of momentum equation between the three cross-sections presented below and illustrated in Figure 3:
1. From Section 2 to BR
2. From BR D to BR U
3. From BR U to Section 3
Figure 3: Conceptual layout of cross-sections for bridge momentum calculations; flow is from left to right (Figure 5-3 of the Hydraulic Reference Manual). Note, this represents the standard 4 cross section layout for bridges as explained in the manual. Sections 1 and 4, which are not displayed in this figure, represent the locations where full flow expansion (Section 1) and beginning of flow contraction (Section 4) occur.
Except for the calculation from Section BU to Section 3 which also includes a term for pier drag, the other two calculations are modified forms of the momentum equation provided as equation 2-37 in the Hydraulic Reference Manual:
Where,
· Βd, βu = Momentum correction coefficient accounting for non-uniform velocity profiles at downstream section (denoted with a subscript d) and the upstream section (denoted with a subscript u) respectively
· Ad, Au = Flow area at downstream and upstream sections, respectively
· g = Acceleration due to gravity
· L = Distance between the downstream and upstream sections along the x-axis
· Qd, Qu = Discharge at downstream and upstream sections, respectively
· S0 = Slope of the channel, based on mean bed elevations
· Sf = Slope of the energy grade line
· Yd, Yu = Depth from the water surface elevation to the centroid of the flow area at the downstream and upstream section, respectively
With a few minor differences in the units and arrangement of terms, this should look very similar to the classic one-dimensional form of the conservation of momentum equation. So, again, why are the two methods calculating such different results? The answer: the weight component, the third term in the equation above (with So) is “off” by default. With some math, the weight component can be resolved to a form that is familiar from introductory fluids: the hydrostatic force acting in the x-direction on an inclined plane. In very simplified terms, this component accounts for a non-level channel bed in the momentum calculations. It can be turned “on” from Geometry -> Bridge/Culvert Data -> Options -> Internal Bridge Momentum -> Add Weight Component, as illustrated in Figure 4:
Figure 4: Location of the bridge momentum equation options menu
Let’s look at our results now, in Figure 5. You can’t see the difference because they are identical, at least for this simple example. They will be slightly different in most applications because of the contraction and expansions losses included in the energy method, but if the flow area of the two cross-sections are fairly similar, the contraction and expansion losses will be small and the two results near-identical.
Figure 5: Comparison of bridge modeling results between energy and momentum methods when the weight component is included.
Easy fix, right? However, the takeaway from this blog post is not to simply check the “include weight component” option. That would be too easy, so please keep reading.
After toggling “on” the weight component, you may notice this error message for certain bridges: “The bridge momentum weight force was very large. Due to the large value of the weight force, the program ignored the weight force during the momentum calculations.” Or, “During momentum computations with the weight force on, an upstream energy was computed lower than the downstream energy. The weight force was turned off and the momentum answer was re-calculated.” In both cases, the weight component is automatically turned off in the calculation. What you end up with, in simple terms, is an assumption of a flat, level channel in the momentum calculation which may yield a different water surface elevation similar to that in Figure 1.
On a reach-scale, the average bed slope is often small, as is the subsequent weight force, and turning “off” the weight component is arguably justifiable. However, on the scale of section-to-section, the bed slope of natural rivers may be significant due to river morphology (pools, riffle), scour holes, natural and artificial controls, and other factors. In Figure 1, the change in bed elevation is about 1.50 ft (compared to a water depth of 20 feet) – not out of the ordinary for a natural cross-section. The resulting slope is approximately 0.03 and the impact on the energy grade line by excluding the weight component is 1.49 feet. That slope is fairly high, but still less than about ~6 degrees (or 10 percent), which is the upper limit for the assumption of a hydrostatic pressure distribution (also adopted by HEC-RAS).
Back to the topic at hand. We know how excluding the weight component affects the implementation of the momentum equation, we know how to have HEC-RAS calculate it, and we know the equation HEC-RAS uses to calculate it, so why should we be concerned if HEC-RAS tells us the weight force was turned off? Well, HEC-RAS automatically excluding weight does not mean that it’s justifiable to ignore the weight component – just that the weight component “doesn’t make sense”. HEC-RAS is giving you, the modeler, a warning that something is not quite adding up and it is up to you to decide if the ensuing results are justifiable. The reason for the results including the weight component “not making sense” is that the weight component is easy to compute for a prismatic channel, but much more difficult for natural cross-sections. What’s the average bed slope between the natural channel cross-sections in Figure 6? Is it the same for baseflow conditions as it is for a high-flow, or does it change with flow depth? Herein lies the challenge.
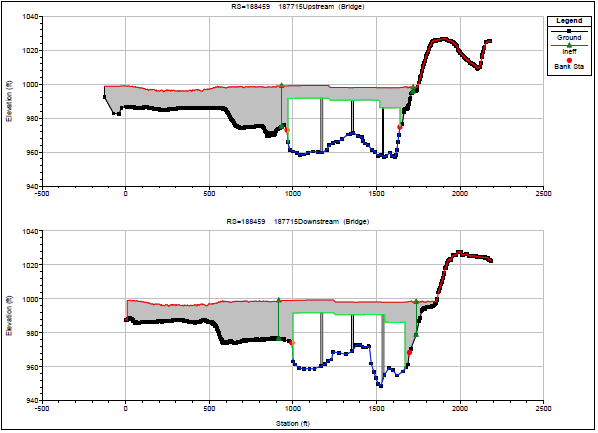
Figure 6: Natural river channel cross-sections
HEC-RAS calculates the bed slope as the difference in average bed elevation between cross-sections divided by the distance between the sections. The average bed elevation of each cross-section is calculated as the critical water surface elevation minus the corresponding hydraulic depth (area divided by top width) for that water surface elevation. Critical depth is used because it produces the same hydraulic depth for cross sections that are identical (versus using the computed water surface elevation to compute hydraulic depth, which may result in different average bed elevations). This is a good approximation in a lot of conditions where there is a gradual change in cross-section shape, but there are several conditions where the calculated weight force will be “too large” and result in an answer that may not “make sense” to HEC-RAS. In particular, I’ve encountered this at bridges with lower Froude numbers where the change in bed elevation is about 5 percent or more of the flow depth; I’m sure there are exceptions and additions to this.
Now that we know that weight is not included in the momentum calculations (by choice or default), the key question is: considering all the sources of uncertainty in development of a model, does not including the weight component have a significant effect on our results? The answer: it depends. As always, the best decisions are informed ones. Let’s take a conceptual look at how the calculated water surface elevations will change when weight component is excluded. For most applications, when the downstream bed elevation is lower than the upstream bed elevation, excluding the weight component will cause the upstream water surface elevation to increase to balance the momentum equation; this is what occurs in Figure 1. However, it would be opposite for an adverse slope. When the average bed elevation increases in the downstream direction, the weight component would be negative in the equation above and the upstream water surface elevation would decrease to balance the equation.
Now, back to whether it’s significant. Take another look at Figure 1. Almost all the energy loss and change in water surface elevation occurs between BR D and BR U. From the discussion above, we know that pier drag is not considered until BR U to Section 3. There is another way to model the energy losses between these particular cross-sections that works quite well for these conditions: the energy method. Referencing Figure 1, we see that the energy method calculates significantly less energy loss than the momentum method (without weight) and we can estimate the impact of excluding the weight component as the difference in EGL at Section 3 after setting the pier drag coefficient to 0.001 in the momentum method, to minimize the effect of pier drag on the resulting calculation. If that difference is significant in comparison to our model tolerance, then the answer is that yes, excluding the weight component is significant to our modeling. As a real-world example, for the “real model” that I based this simplified model on, including or excluding the weight component was a 1.0 ft difference in the water surface elevation at Section 3. This 1.0 ft difference was equivalent to approximately 1.5 miles of cumulative energy losses in the upstream reach and was also the difference between a proposed $4 million floodplain bridge being cost-effective or not to reduce upstream flood depths. Toggling the weight component on or off was very significant to the upstream community!
If you have stuck with me thus far and have determined that the impact of excluding the weight component is significant to your model, and HEC-RAS automatically turns the weight component off, there are several options for modeling Class A low-flow conditions. In the preferred order of application:
1. If the bridge has no piers, the energy method will provide satisfactory results. Under Class A flow conditions, the key difference between the momentum method and energy method is that drag effects imparted by the piers are accounted for in the momentum method whereas they are not in the energy method (only the obstruction of flow area).
2.
2. For cases where BR U and BR D have been copied from Section 2 and Section 3, the magnitude of the weight component can be decreased by vertically adjusting the BR D and BR U cross-sections up-or-down to spread out the change in bed elevation. The HEC-RAS default for the geometry of BR D and BR U is to copy the exact geometry from Section 2 and Section 3, respectively. As a result, whatever the average change in bed elevation between Section 2 and Section 3 was now occurs between BR U and BR D. This decrease in the length over which the change in bed elevation occurs increases the average bed slope and therefore the weight component. Unless it is known that the change in bed elevation does occur only between BR U and BR D, spreading out the change between cross-sections will decrease the maximum weight force in the three set of calculations and may yield a solvable solution to the momentum equation including the weight component. Worst case, if the weight component is still excluded, it will generally decrease the impact of excluding the weight component; Figure 7 provides a comparison of these water surface profiles.
3. If the bridge has piers and the energy losses from pier drag are not significant, the energy method may reasonably be used to estimate hydraulic losses through the bridge. The magnitude of energy losses from pier drag can be estimated from the momentum equation method by changing the pier drag coefficient to 0.001 (to minimize the impact of the pier drag on calculations between BR U and Section 3) and calculating the resultant change in EGL at Section 3. If this value is less than the tolerance for your application and less than the change in EGL by excluding the weight component, it may be justifiable to proceed with the energy method only. Please note this method is an approximation only, as inclusion of the weight component would affect the cross-section velocity that is squared in the calculation of pier drag losses, this estimation will be increasingly inaccurate at higher velocities.
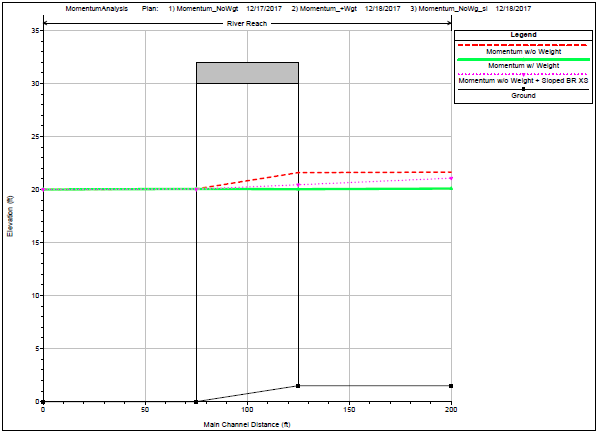
Figure 7: Bridge modeling results for momentum method: with weight component (green), without weight component (red), and Alternative 2 “spread out the slope” without weight component (magenta).
There you have it – more detail than you ever thought you would need on one small component of one routine in HEC-RAS! However, as we can see this one small component can sometimes have significant effects on hydraulic models that should be considered. At a minimum, we need to understand that when the bed slope decreases downstream, excluding the weight component may overestimate upstream water depth and underestimate velocity. The opposite is true for an adverse slope. The post above is by no means the end-all-be-all for hydraulic modeling of bridges, it is merely to better inform modelers of the effect of the option to include the weight component in model calculations, so please continue to consider calibration data, high/pressure flow, supercritical flow, unsteady hydrographs, and other considerations in your selection of a bridge modeling approach!
This post was written by James Woidt, PE, a senior project engineer in the Scarborough, ME office of Woidt Engineering and Consulting. Mr. Woidt would like to acknowledge Gary Brunner, PE for his contributions to this article.
Comments
Add Your Comment