User-Defined Gate Opening Rating Curves

[sktse]

I’m doing a dam breach scenario with gate openings at various heights, and I’m having trouble understanding the calculation.

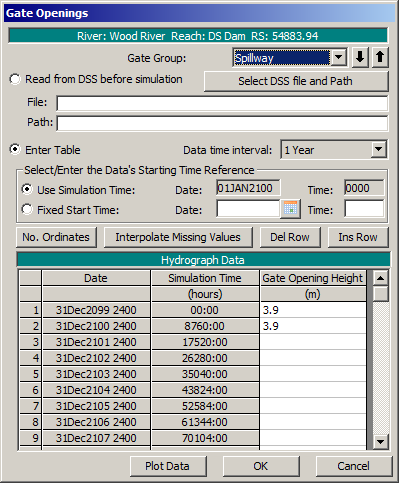
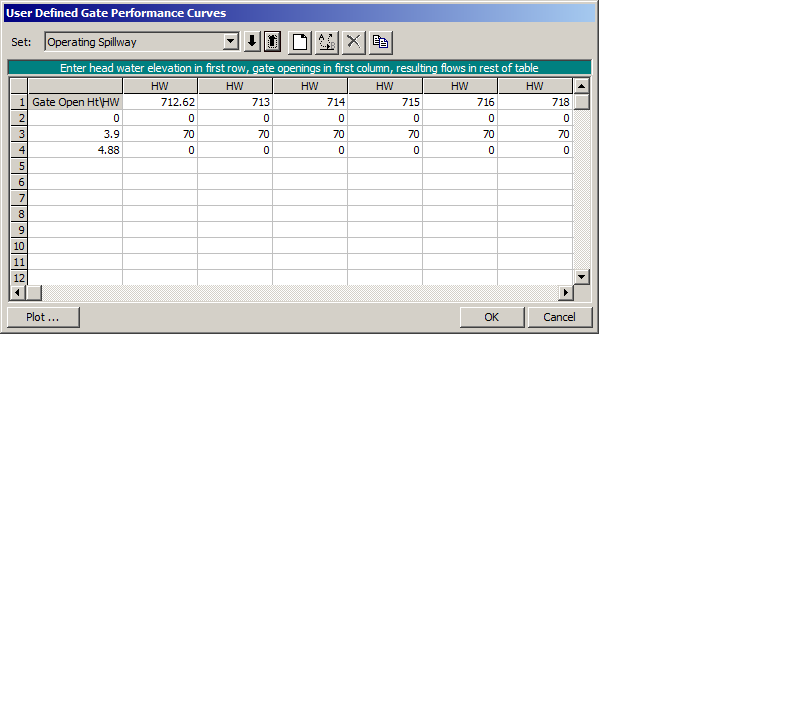
As a sandbox test, I created a user-defined gate opening rating curve where, at 3.9 m, it has a flat discharge of 70 m3/s. I set the inline structure to have a pilot flow of 10 m3/s, and 5 gate openings. I’ve set the gate openings to be stuck at 3.9 m for the whole year.

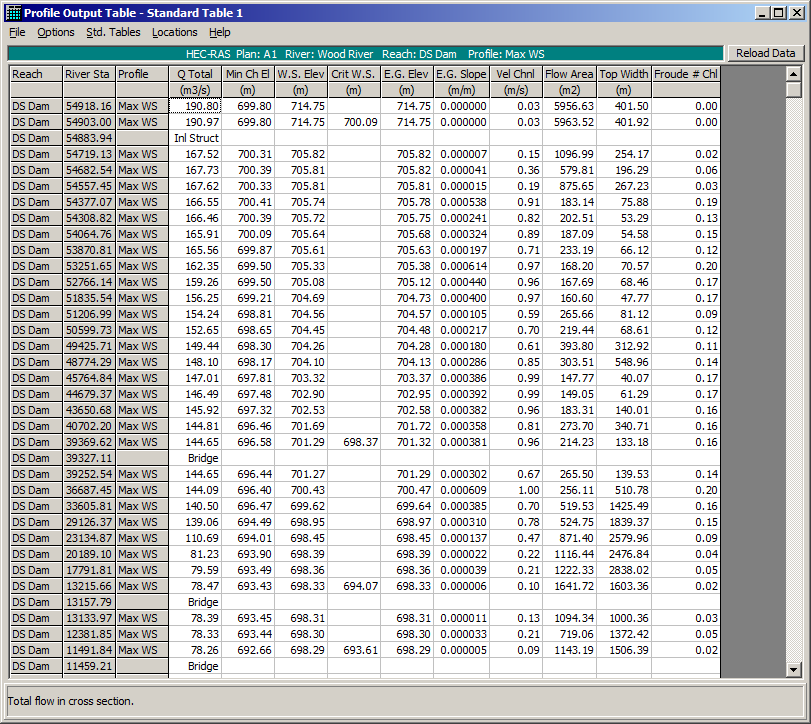
With these parameters, I expect that the total flow in the d/s end to be 70*5 = 350 m3/s or 360 m3/s with the pilot flow. However, when I run the unsteady model, I’m getting a value of 167.52 m3/s, and I’m confused how this number was calculated. Because the rating curve is a constant 70 m3/s, shouldn’t the flow be the same regardless of the headwater height (which in this case was 714.75 m)? Can anybody help me out here?

Many thanks.

[Anonymous]

Is the gate opening submerged? If the water surface is lower than the top of the gate opening, then it uses the depth of the water for the lookup (I’ve been confused by this before). So if the water surface is only 1.95 meters above the gate invert, then you would get 35 m3/s not 70 m3/s.
Also, I think the pilot flow is treated as a minimum as opposed to an additional flow.

[sktse]

This sounds like a good match for what I’m seeing here. I looked up the v4.1 Hydraulic Reference Manual and I noticed the note on 8-11.

However, it uses an equation here Q = CLH^(3/2) that has parameters I have not entered.

C = Weir Coefficient
L = Length of spillway Crest
H = Upstream energy head above the spillway crest (in this case it would be 714.75 m – 712.62 m = 2.13 m i suppose?)

If I assume that C = 1.4 and L = 7.2 m based on the values that I enter on the inline structure (but that don’t necessarily apply to the gate openings), then I get:

Q = (1.4)*(7.2 m)*(2.13 m)^(3/2) = 31.33 m3/s

This does appear to be in the right ballpark. I’ll have to do more playing around with this.

[Author]

Posts